Problem

Problem ID: 1352

Title: Maximum Profit in Job Scheduling

Difficulty: Hard

Description:

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

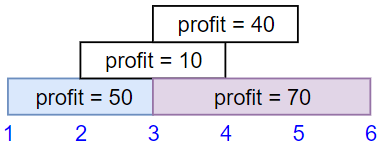
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

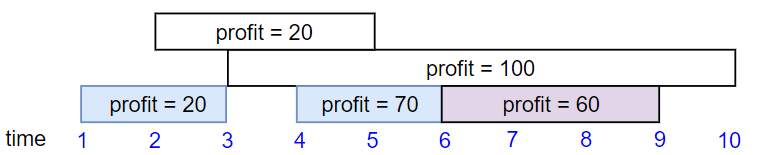
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 104
• 1 <= startTime[i] < endTime[i] <= 109
• 1 <= profit[i] <= 104

Thoughts

This question is similar to 1851 where you need to use DP to optimise for both value and end time. Tried to use size_t for all indexes but it leads to integer underflow and had to add an underflow check before -1. Not sure what is the cleaner way to do binary search with size_t.

Solution

General Idea

We treat all endTimes as the only possible times in the problem. When deciding on whether or not to choose a job, we can either choose it with the best possible combinations of jobs with endTime < starTime or not choose it and have the profit set to the previously calculated best combinations of jobs.

DP State: dp[i] - represents the best profit as of jobs[i].endTime

DP transitions: We can either

• Drop the current job: dp[i] = dp[i-1]
• Choose the current job: dp[i] = dp[k] + jobs[i].profit where k is the largest index such that jobs[k].endTime <= jobs[i].startTime

Implementation

struct Job {
    int start;
    int end;
    int profit;
};
class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        auto n = startTime.size();
        vector<Job> jobs(n);
        for (size_t i = 0; i < n; i++) {
            jobs[i] = {startTime[i], endTime[i], profit[i]};
        }
        
        sort(jobs.begin(), jobs.end(), [](const auto& a, const auto& b) { return a.end < b.end; });
        vector<int> dp(n, 0);
        
        for (auto i = 0; i < n; i++) {
            int prev_profit = i > 0 ? dp[i-1] : 0;
            const auto [start, end, profit] = jobs[i];
            size_t l = 0;
            size_t r = n-1;
            while (l < r) {
                size_t m = (l+r + 1)/2;
                if (jobs[m].end <= start) {
                    l = m;
                } else {
                    r = m;
                    if (r != 0) r--;
                }
            }
            int curr_profit = profit;
            if (jobs[l].end <= jobs[i].start) curr_profit += dp[l];
            dp[i] = max(curr_profit, prev_profit);
        }
        return dp[n-1];
    }
};