Problem

Problem ID: 1851

Title: Maximum Number of Events That Can Be Attended II

Difficulty: Hard

Description:

You are given an array of events where events[i] = [startDayi, endDayi, valuei]. The ith event starts at startDayi and ends at endDayi, and if you attend this event, you will receive a value of valuei. You are also given an integer k which represents the maximum number of events you can attend.

You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.

Return the maximum sum of values that you can receive by attending events.

Example 1:

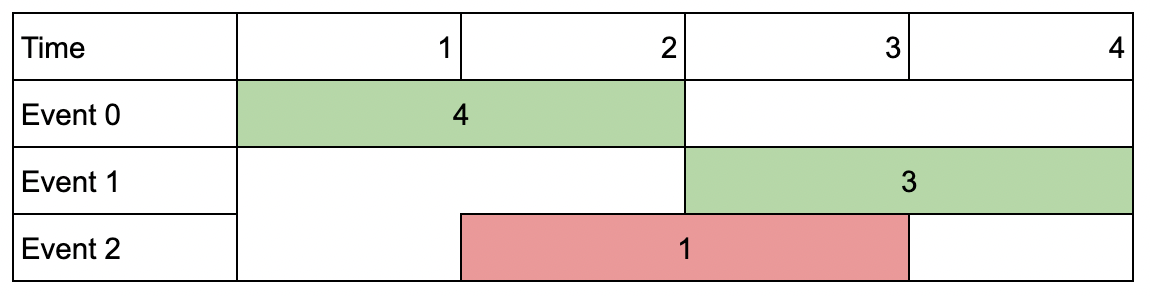
Input: events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
Output: 7
Explanation: Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.

Example 2:

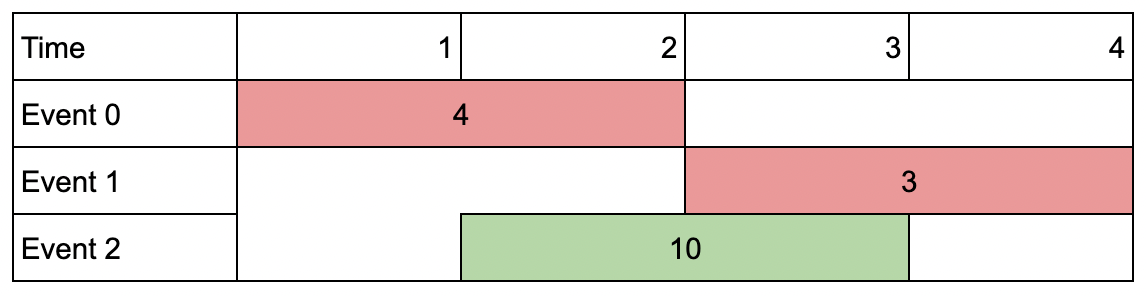
Input: events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
Output: 10
Explanation: Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do not have to attend k events.

Example 3:

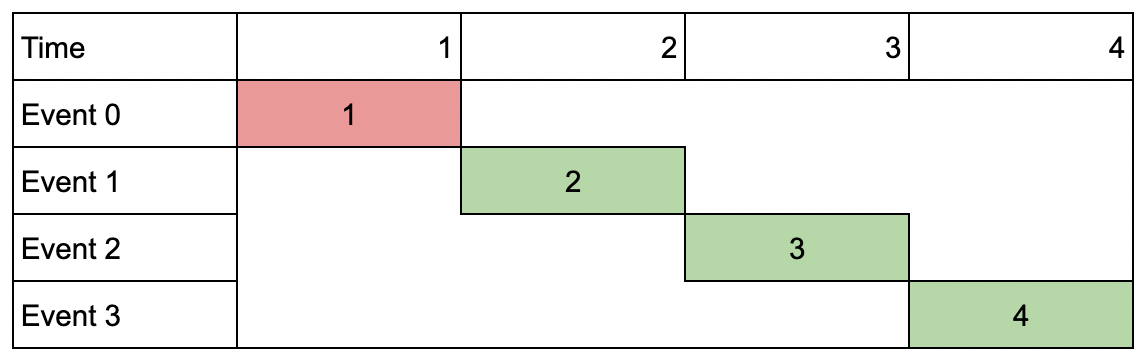
Input: events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
Output: 9
Explanation: Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.

Constraints:

• 1 <= k <= events.length
• 1 <= k * events.length <= 106
• 1 <= startDayi <= endDayi <= 109
• 1 <= valuei <= 106

Thoughts

I had difficulty solving this problem as initially I was not sure how to optimise for value and end time for the DP transition. Knowing that k*events.length < 1e6 was a big hint as it implies that the problem should be solved using a 2DP of n times k.

Solution

General Idea We will use bottom up DP to solve this problem with the following state and transitions. The reason we have to use DP instead of greedy is because choosing event i could result in later overlapping events with large value(INF) being passed on but passing on event i could result in a wrong answer if event i has (INF) value.

DP State - dp[i][j]

• Represents the maximum score at the end of events[i]’s end time with j events selected.

DP Transition - when processing event i we could:

• Choosing current event:
  • Logically, this means choosing the current events with the maximum valid combination of previous events that do not overlap with the current event.
  • The value will be equals to events[i]’s value sum with dp[k][j-1] where k is the event with end time strictly less than the current event start time.
  • dp[k][j-1]: represents a combination of j-1 previous events that has the maximum value and do not overlap with the current event
• Passing on the current event:
  • Value Equals to dp[i-1][j] as it represents the combination of previous j events
• Final dp transition: dp[i][j] = max(dp[i-1][j], events[i][2] + dp[k][j-1])

Implementation

class Solution {
public:
    int maxValue(vector<vector<int>>& events, int k) {
        events.push_back({0,0,0});
        int n = events.size();
        sort(events.begin(), events.end(), [](const auto& a, const auto& b){return a[1] < b[1];});
        vector<int> end_times(n,0);
        for (int i = 0; i < n; i++) end_times[i] = events[i][1];

        vector<vector<int>> dp(n, vector<int>(k+1, 0));
        int ret = 0;
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < k+1; j++) {
                auto it = lower_bound(end_times.begin(), end_times.end(), events[i][0]);
                assert(it != end_times.end());
                assert(it != end_times.begin());
                it--;
                int k = std::distance(end_times.begin(), it);
                dp[i][j] = max(events[i][2] + dp[k][j-1], dp[i-1][j]);
                ret = max(ret, dp[i][j]);
            }
        }
        return ret;
    }
};